11  Estimating with Confidence a Single Mean

Consider the Birth Weight Case Study described in Chapter 9. In the previous chapter, we introduced the following model for how birth weights for infants are generated:

\[(\text{Birth Weight})_i = \mu + \varepsilon_i\]

where \(\mu\) represents the average birth weight of infants born in North Carolina. We also discussed imposing two conditions on the distribution of the random error terms:

Within this model for the data generating process, \(\mu\) is an unknown parameter of interest. Consider the following research goal associated with this parameter:

On average, what is the birth weight of an infant born in North Carolina?

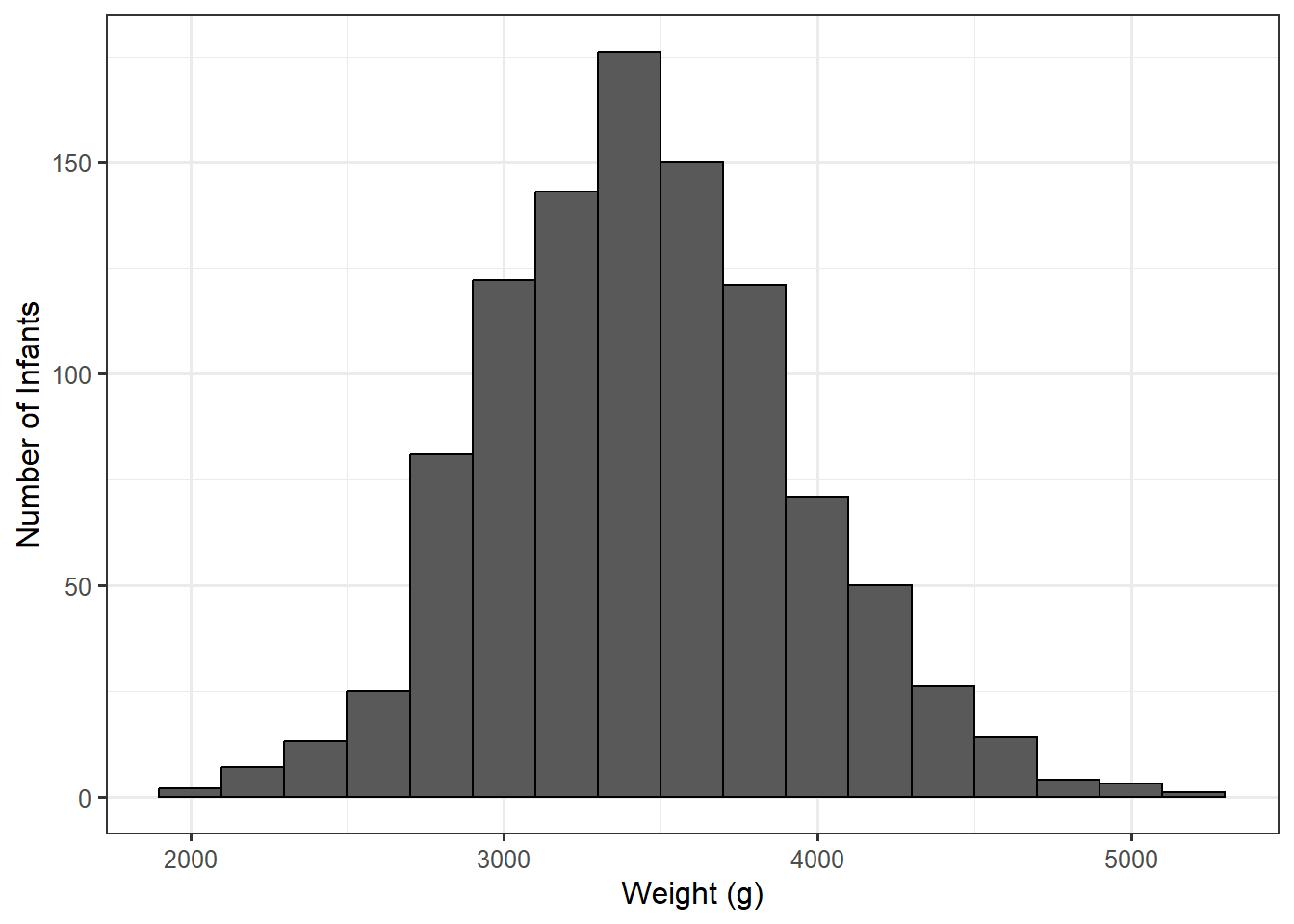
We can construct a point estimate of the parameter \(\mu\) with the average birth weight of infants in our sample: 3448.26 g. The data is graphically summarized in Figure 11.1.

Histogram of the weight, in grams, of infants born in North Carolina; the peak is near 3500 grams.
Figure 11.1: Weight of a sample of full-term infants born in North Carolina.

In order to construct an estimate of \(\mu\) which incorporates the variability in the sample mean, we must model the sampling distribution of our estimate. The bootstrap procedure for this case would be

  1. Randomly sample, with replacement, 1009 records from the original sample.
  2. For this bootstrap resample, compute the mean birth weight and retain this value.
  3. Repeat steps 1 and 2 many (say 5000) times.

This process is illustrated in Table 11.1. Each row represents the birth weights for a single resample taken with replacement from the original data. The final column is the computed (and retained), sample mean from each resample (the bootstrap statistic).

Table 11.1: Partial printout of first 10 bootstrap resamples and the resulting bootstrap statistic.
Value 1 Value 2 Value 3 Value 1007 Value 1008 Value 1009 Boostrap Mean
3345 3572 3572 ... 3827 3827 3119 3461.89
3629 2892 3827 ... 4111 3374 2948 3476.69
2495 3686 3827 ... 3289 3544 3487 3428.90
3856 3430 3771 ... 3487 3742 2665 3436.20
3430 3119 4479 ... 3686 3090 3005 3451.09
3289 3459 3827 ... 3600 3856 3260 3473.89
2863 3345 3232 ... 3345 3544 2948 3427.89
3289 4026 3856 ... 4338 3771 3714 3435.78
3175 3544 3771 ... 3572 3515 3005 3419.37
3260 3771 3742 ... 3572 4054 3033 3447.77

A plot of the resulting bootstrap sample means is shown in Figure 11.2. Notice that the x-axis is different from that of Figure 11.1. While a graphical summary of the raw data is summarizing the weight of individual infants, the model for the sampling distribution is summarizing the statistic we compute in various resamples of the same size. In Figure 11.2, we are not keeping track of individual infant weights but average weights for collections of 1009 infants.

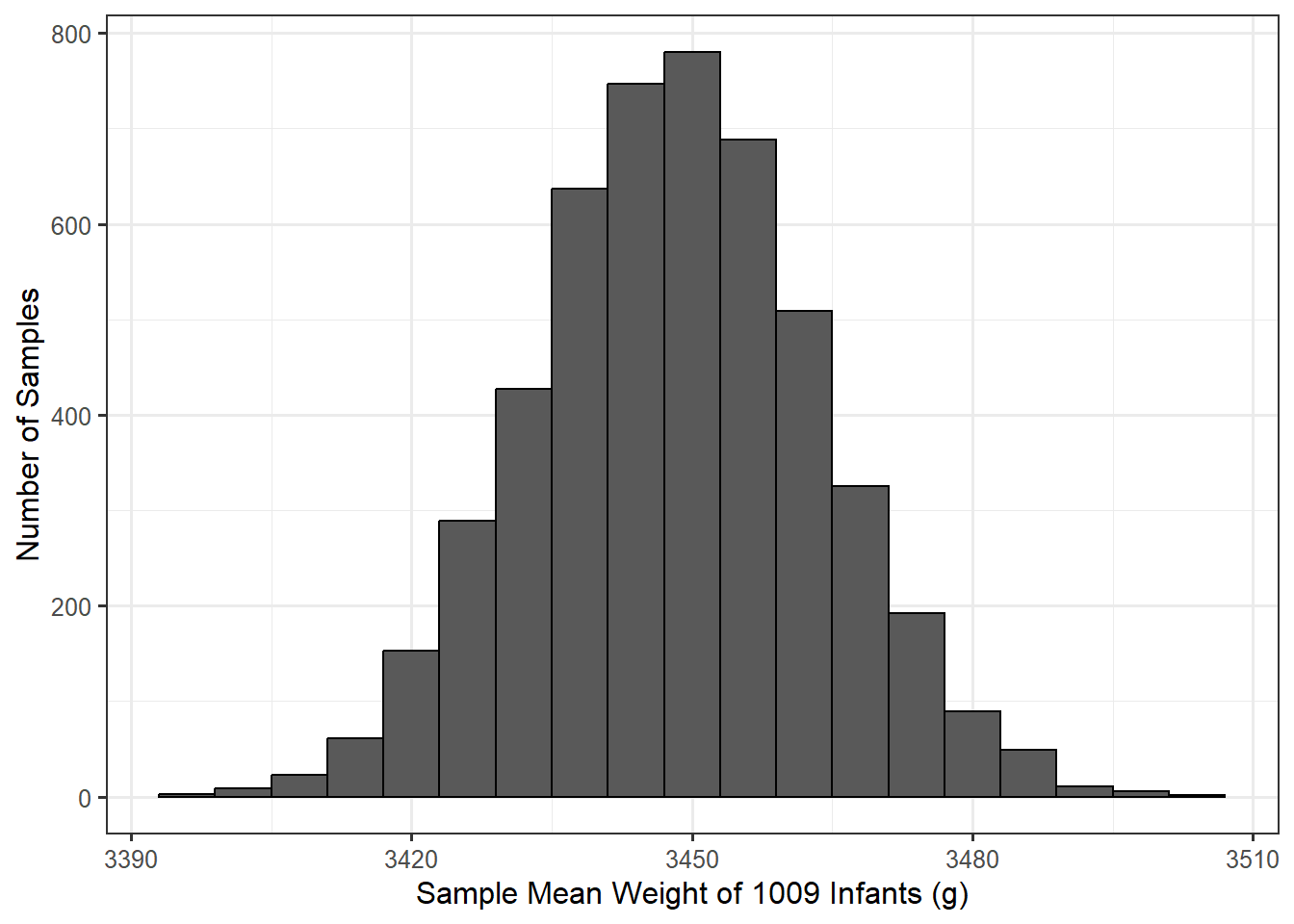
Histogram of bootstrap statistics centered on 3450 and ranging from 3400 to 3500.
Figure 11.2: Bootstrap model for the sampling distribution of the average birth weight for a sample of 1009 infants born in North Carolina.

Using this model for the sampling distribution, we can then grab the middle 95% of values in order to construct a confidence interval for the parameter of interest. This results in a 95% confidence interval of (3418.73, 3479). Based on this confidence interval, the data is consistent with the birth weight of infants in North Carolina, on average, being between 3418.73 and 3479; that is, these are the reasonable values of the mean birth weight.

Notice that we are able to narrow down the reasonable values of the parameter to a relatively small interval (a difference of about 60 grams). This is not because all babies in North Carolina have an extremely similar birth weight. It is because we have a relatively large sample, allowing us to have high confidence in our estimate of the average birth weight of an infant. The confidence interval does not tell us where we expect an individual infant’s birth weight to fall; it only communicates what we are estimating the average birth weight of all infants to be based on our observed sample.

Also, notice how much narrower the model for the sampling distribution is compared to the distribution of the variable in the sample. Remember, statistics have less variability than individual values. This also illustrates why a confidence interval could never describe the fraction of values in the population which fall within a certain range — the variability is not comparable because a sampling distribution has a different x-axis than the distribution of the population or sample.